문제 설명
•
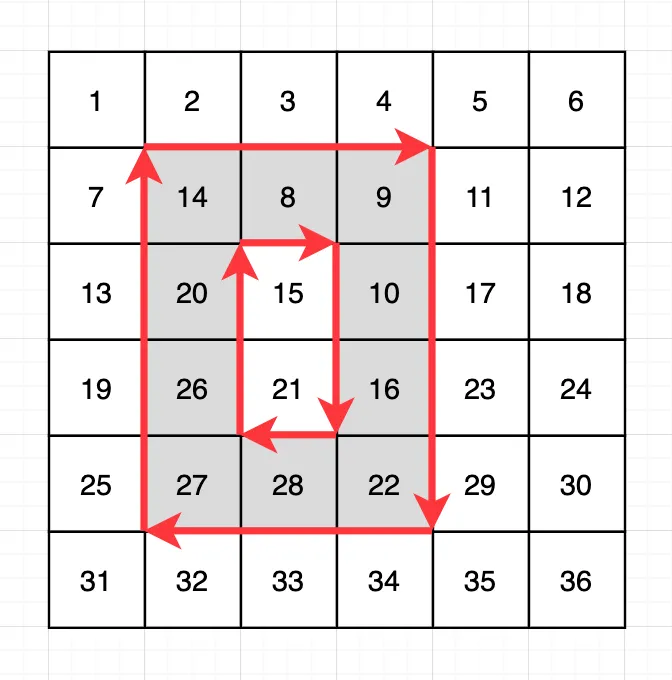
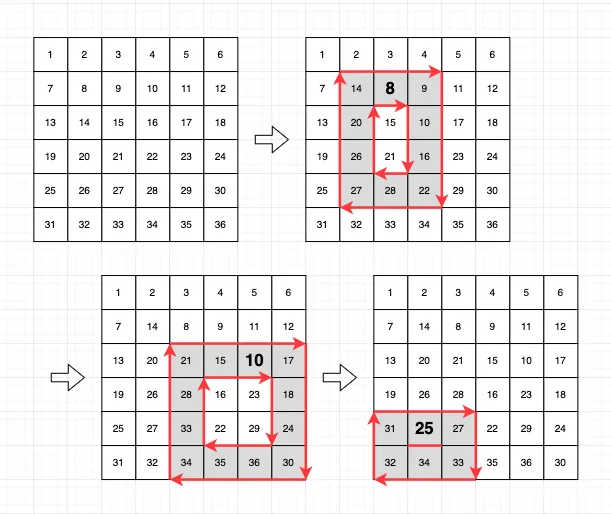
주어진 범위의 행렬 테두리 숫자들을 시계방향으로 회전시키고, 각 회전마다 최소값을 구하는 문제
◦
처음에 행렬에는 가로 방향으로 숫자가 1부터 하나씩 증가하면서 적혀있다.
예제 입력/출력
rows | columns | queries | result |
6 | 6 | [[2,2,5,4],[3,3,6,6],[5,1,6,3]] | [8, 10, 25] |
3 | 3 | [[1,1,2,2],[1,2,2,3],[2,1,3,2],[2,2,3,3]] | [1, 1, 5, 3] |
100 | 97 | [[1,1,100,97]] | [1] |
제약 조건
•
rows는 행렬의 세로 길이(행 개수)
◦
•
columns는 행렬의 가로 길이(열 개수)
◦
•
queries는 회전시킬 영역을 나타내는 쿼리들의 목록
◦
◦
각 query는 4개의 정수로 이루어져 있으며, 순서대로 (x1, y1, x2, y2)를 나타낸다.
▪
▪
◦
모든 query는 유효한 범위 내에서 주어진다.
문제 풀이
브루트 포스 -
풀이 코드
def rotate_side_number(y1, x1, y2, x2):
global matrix
# 테두리 영역 좌표 값 수집
pos = []
for x in range(x1, x2 + 1):
pos.append((y1, x))
for y in range(y1 + 1, y2 + 1):
pos.append((y, x2))
for x in range(x2 - 1, x1 - 1, -1):
pos.append((y2, x))
for y in range(y2 - 1, y1, -1):
pos.append((y, x1))
N = len(pos)
# 회전
for i in range(N - 1, 0, -1):
ny, nx = pos[i][0], pos[i][1]
y, x = pos[i - 1][0], pos[i - 1][1]
matrix[ny][nx], matrix[y][x] = matrix[y][x], matrix[ny][nx]
return min(matrix[y][x] for y, x in pos)
def solution(rows, columns, queries):
global matrix
# Init
matrix = [[0 for _ in range(columns + 1)] for _ in range(rows + 1)] # 1-Index
for i in range(1, rows + 1):
for j in range(1, columns + 1):
matrix[i][j] = (i-1) * columns + j
# Solve
answer = []
for query in queries:
y1, x1, y2, x2 = query
min_num = rotate_side_number(y1, x1, y2, x2)
answer.append(min_num)
return answer
Python
복사