Search

PGS 도넛과 막대 그래프

태그
그래프 이론
그래프 탐색
생성일
2024/12/11 12:13

문제 설명

•
주어진 방향 그래프의 간선 정보를 바탕으로, 생성된 정점의 번호와 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 개수를 구하는 문제

예제 입력/출력

입출력 예 #1

edges
result
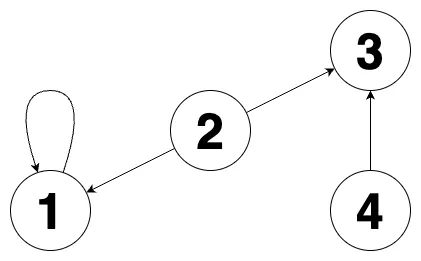
[[2, 3], [4, 3], [1, 1], [2, 1]]
[2, 1, 1, 0]

입출력 예 #2

edges
result
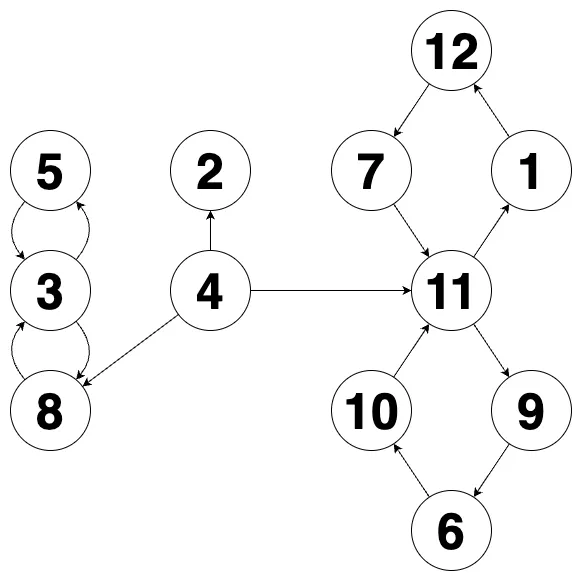
[[4, 11], [1, 12], [8, 3], [12, 7], [4, 2], [7, 11], [4, 8], [9, 6], [10, 11], [6, 10], [3, 5], [11, 1], [5, 3], [11, 9], [3, 8]]
[4, 0, 1, 2]

제약 조건

•
1≤∣edges∣≤1,000,0001 ≤ |edges| ≤ 1,000,000
◦
edgs의 원소는 [a, b]의 형태이며, a→b 정점으로 향하는 간선이 있음을 의미
◦
1≤ a, b ≤1,000,0001 ≤ a, b ≤ 1,000,000
•
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상

문제 풀이

•
노드와 간선의 범위
◦
∣edges∣≤1,000,000|edges| \leq 1,000,000
◦
∣nodes∣≤1,000,000|nodes| \leq 1,000,000
풀이1 각 노드의 출발과 도착 간선 수를 계산하여, 그래프 종류 파악 - O(∣edges∣)O(|edges|)
풀이2 부분 그래프의 노드와 간선의 개수를 계산하여, 그래프 종류 파악 - O(∣nodes∣+∣edges∣)O(|nodes| + |edges|)

풀이 코드

풀이1 각 노드의 출발과 도착 간선 수를 계산하여, 그래프 종류 파악 - O(∣edges∣)O(|edges|)
풀이2 부분 그래프의 노드와 간선의 개수를 계산하여, 그래프 종류 파악 - O(∣nodes∣+∣edges∣)O(|nodes| + |edges|)

참고 자료