문제 설명
•
지점 수와 등산로, 출입구, 산봉우리 정보가 주어질 때, 출입구에서 시작해 산봉우리 한 곳을 방문하고 돌아오는 코스 중 intensity가 최소인 코스를 찾아, 해당 산봉우리 번호와 intensity 최솟값을 반환하는 문제
◦
intensity : 특정 등산코스에서 휴식 없이 연속으로 이동해야 하는 구간 중 가장 긴 이동 시간을 의미
▪
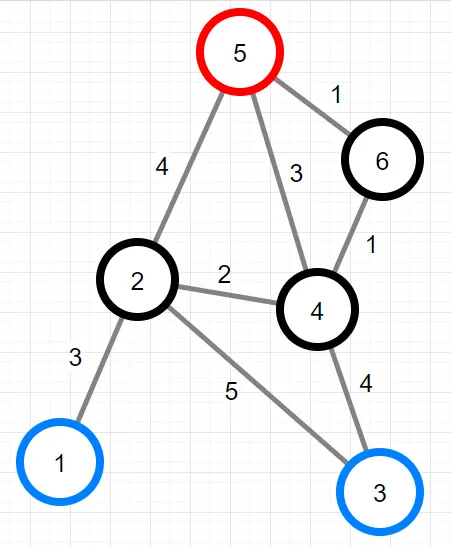
해당 코스에서 intensity 값은 5
▪
해당 코스에서 intensity 값은 3
예제 입력/출력
n | paths | gates | summits | result |
6 | [[1, 2, 3], [2, 3, 5], [2, 4, 2], [2, 5, 4], [3, 4, 4], [4, 5, 3], [4, 6, 1], [5, 6, 1]] | [1, 3] | [5] | [5, 3] |
7 | [[1, 4, 4], [1, 6, 1], [1, 7, 3], [2, 5, 2], [3, 7, 4], [5, 6, 6]] | [1] | [2, 3, 4] | [3, 4] |
7 | [[1, 2, 5], [1, 4, 1], [2, 3, 1], [2, 6, 7], [4, 5, 1], [5, 6, 1], [6, 7, 1]] | [3, 7] | [1, 5] | [5, 1] |
5 | [[1, 3, 10], [1, 4, 20], [2, 3, 4], [2, 4, 6], [3, 5, 20], [4, 5, 6]] | [1, 2] | [5] | [5, 6] |
제약 조건
•
•
◦
의 원소는 [i, j, w]
◦
◦
서로 다른 두 지점을 직접 연결하는 등산로는 최대 1개
•
•
문제 풀이
•
노드와 간선의 범위
◦
◦
접근1 모든 경우를 살펴보는 브루트 포스 적인 풀이 -
접근2 파라매트릭 서치 -
접근3 다익스트라 -
풀이 코드
접근2 파라매트릭 서치 -
접근3 다익스트라 -