문제 설명
•
5개의 대기실에서 응시자들이 거리두기를 잘 지키고 있는지 판별하는 문제
[방역 규칙]
1.
대기실은 5개이며, 각 대기실은 5x5 크기입니다.
2.
거리두기를 위하여 응시자들 끼리는 맨해튼 거리가 2 이하로 앉지 말아 주세요.
•
맨해튼 거리:
3.
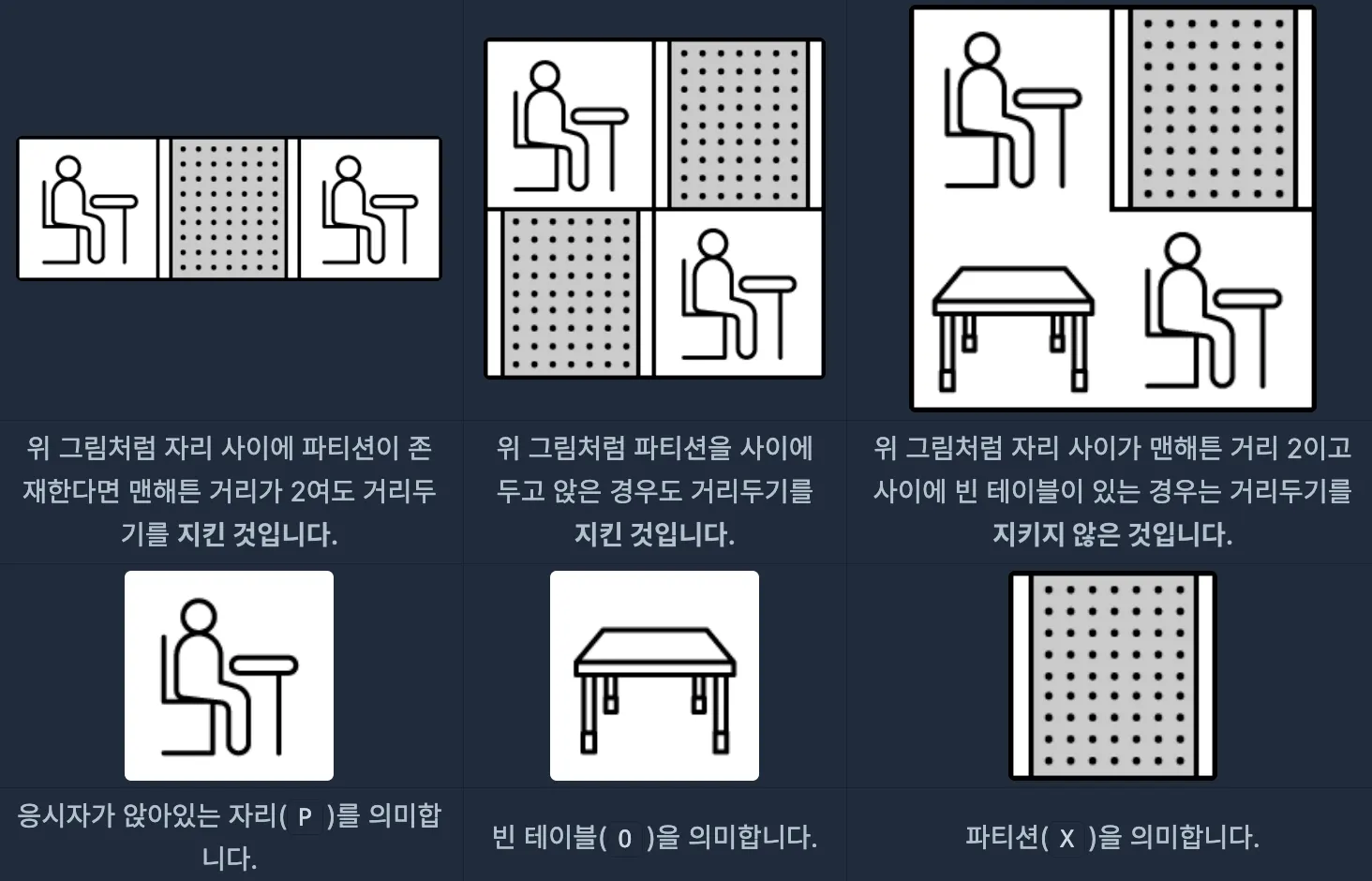
단, 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.
예제 입력/출력
places | result |
[["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"], ["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"], ["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]] | [1, 0, 1, 1, 1] |
제약 조건
•
대기실 개수 =
◦
각 대기실 크기 =
문제 풀이
•
접근1 브루트 포스 - 상한
◦
문제에서 요구하는 조건을 하나씩 체크하며 구현하는 단순 구현 문제
◦
제한된 입력 크기와 조건 때문에 브루트 포스 방식으로 충분히 해결 가능.
◦
거리두기 조건
▪
두 응시자 간의 맨해튼 거리가 2 이하일 경우만 위반 가능성이 있음.
조건에 따라 세부적으로 위반 여부 확인
◦
접근 방식
1.
대기실 내 모든 응시자 위치를 저장
2.
각 응시자 쌍에 대해 맨해튼 거리와 위반 조건을 검사
3.
모든 조건을 만족하면 해당 대기실은 1, 위반이 발생하면 0 반환
풀이 코드
def check_distance(place):
# 응시자 위치를 리스트로 저장
p_list = [(y, x) for y in range(5) for x in range(5) if place[y][x] == 'P']
for y1, x1 in p_list:
for y2, x2 in p_list:
m_dist = abs(y2 - y1) + abs(x2 - x1) # 맨해튼 거리
if m_dist == 1: # 맨해튼 거리가 1일 경우 바로 실패
return 0
if m_dist == 2: # 맨해튼 거리가 2인 경우만 추가 조건 체크
# 같은 행
if y1 == y2 and place[y1][(x1 + x2) // 2] != 'X':
return 0
# 같은 열
if x1 == x2 and place[(y1 + y2) // 2][x1] != 'X':
return 0
# 대각선
if y1 != y2 and x1 != x2:
if place[y1][x2] != 'X' or place[y2][x1] != 'X':
return 0
return 1
def solution(places):
# 각 대기실에 대해 거리두기 여부 확인
return [check_distance(place) for place in places]
Python
복사